Convert Binary ofrece una herramienta online gratuita, que te permite convertir números decimales a su representación binaria.
Al final de esta página hay un tutorial sobre cómo convertir de decimal a binario, léelo si quieres aprender más sobre el proceso de conversión de decimal a binario.
CONVERSIÓN DE DECIMAL A BINARIO
ConvertBinary.com facilita la conversión de números decimales a binario: solo tienes que introducir un número decimal en el formulario de abajo.
Valora este conversor
Características del conversor
| 🔢 Longitud de entrada Decimal: | Hasta 25 dígitos |
| ⚡ Velocidad de conversión: | ¡Instantánea! |
| ➡️ Salida Binaria: | Visualizar, Copiar, Guardar |
| 🎯 Precisión de la conversión: | 100% |
Cómo utilizar el conversor de decimal a binario
Tiempo necesario: 1 minuto
- Introduce el número decimal
Introduce un número decimal en el primer campo.
- Pulsa el botón Convertir
Pulsa el botón Convertir debajo del campo numérico.
- Revisa el resultado
El número binario aparecerá en el segundo campo.
- Copiar o guardar
Opcionalmente, puede copiar el resultado en el portapapeles o guardarlo como un archivo en su dispositivo.
También puedes convertir de binario a decimal.
Cómo convertir de decimal a binario
Si trabajas con ordenadores, puede que necesites una comprensión básica del sistema binario. O quizás quieres aprender binario por diversión. Sea como sea, saber cómo convertir de decimal a binario puede ser una habilidad muy útil.
Y esta es la mejor parte: no necesitas la carrera de matemáticas ni una calculadora de decimal a binario para hacerlo.
Unos y ceros
Puedes considerar el binario como el idioma que hablan los ordenadores. Se compone de una serie de unos y ceros. A simple vista puede parecer una locura, pero tiene su técnica. Empezaremos con una simple cifra de un solo dígito y explicaremos cómo puedes convertir un decimal a binario. Vamos a usar el número 7.
Convertir de decimal a binario supone redefinir el número que quieres convertir. 7 se puede representar simplemente como 7. O se puede representar como 4+3. Reescribir el número es el primer paso para convertirlo en binario. Más específicamente, lo que queremos es diseccionar nuestro número decimal en la suma de potencias de 2.
Veamos el 7, y pensemos en potencias de 2. ¿Qué potencia de 2 es la más cercana al número 7, siendo igual o menor que 7?
2² nos da 4, así que vamos a usar 4 para empezar a descomponer 7. Tenemos que sumarle 3 para llegar a 7. Con lo cual, podemos considerar que 7=4+3.
Puede ser útil tener una tabla de potencias de 2 como referencia. Hemos incluido parte de la tabla en la imagen de abajo.

Ahora nos queda 3, pero no hay potencias de 2 que nos den 3. Tenemos que descomponer 3 de la misma forma que hicimos con 7. Es decir, encontrar la suma de potencias de 2 que nos dará como resultado 3. Recuerda, tenemos que empezar con potencias de 2 iguales o menores que 3. 2¹ nos da 2, y 20 nos da 1.

Hemos usado tres potencias de 2 diferentes en este ejemplo. Con lo cual, la representación binaria de 7 será de tres dígitos de largo. Como la potencia de 2 más alta que necesitamos es 2², vamos a empezar contando cuántas veces hemos usado 2². En binario, solo puede haber dos respuestas a esta pregunta: se ha usado una o cero veces. Si la hemos usado, lo indicamos con un 1. Si no, lo indicamos con un 0.
Haber usado 2² significa que escribimos un 1. Ahora continuamos hacia abajo, contando el resto de potencias de 2 que hemos usado. Hemos usado 2¹, así que lo indicamos con otro 1. Hemos usado 20, así que usaremos 1 para el último espacio.
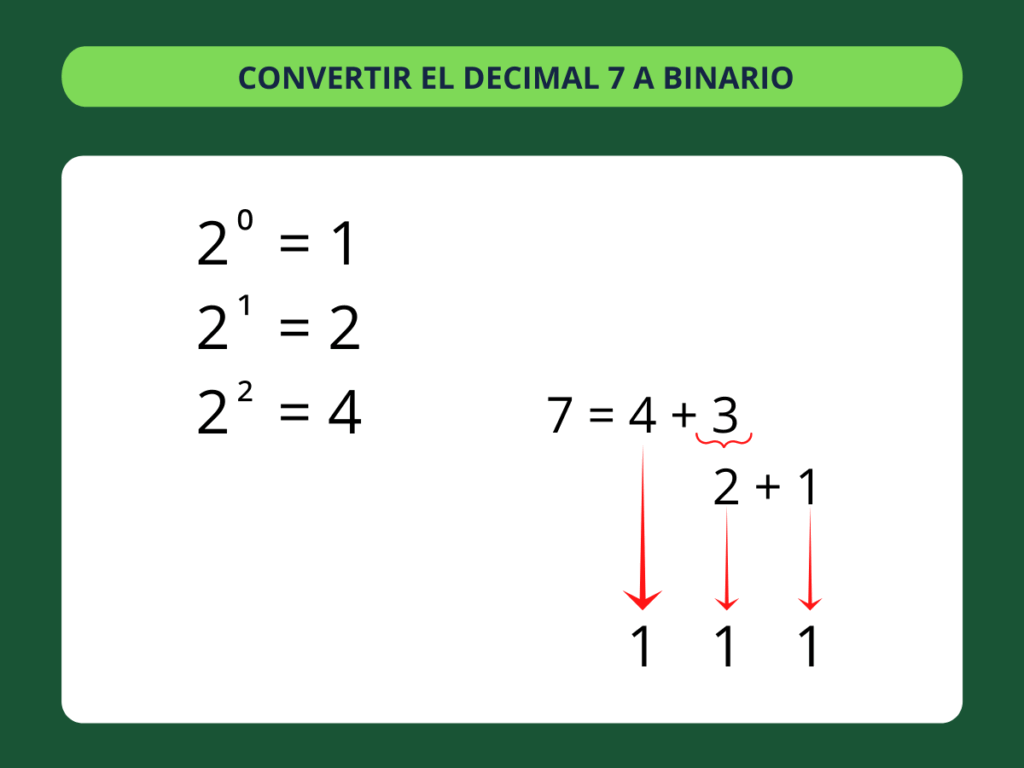
Ya tenemos el decimal 7 convertido en binario, 111.
Podemos usar 8 como un ejemplo incluso más fácil de cómo convertir de decimal a binario. ¿Qué potencia de 2 es igual o menor que 8? 2³ nos da exactamente 8, así que no tenemos que descomponer nada.
Hemos usado 2³ una vez. Hemos usado 2², 2¹, y 20 cero veces. Con lo cual, 8 nos da 1000 en binario. El sistema binario consiste simplemente en contar cuántas veces has usado una potencia de 2 para descomponer tu número decimal.

¿Significa eso que si queremos escribir el decimal 78 en binario, podemos combinar los equivalentes binarios de cada dígito? ¿111 y 1000? Bueno, no es exactamente así. ¡1111000 se traduce a 120! Pero si queremos traducir 78 a binario, es igual de fácil que traducir un decimal de una cifra.
Igual que antes, buscamos la potencia de 2 más cercana a 78. 26 nos da 64, que es lo más cerca de 78 que podemos encontrar sin pasarnos de 78. Podemos redefinir 78 como 78 = 64 + 14.

Ahora también tenemos que redefinir 14. Podemos usar 2³ para obtener 8, y ahora tenemos que sumarle 6 para llegar a 14. Como 6 tampoco es una potencia de 2, tenemos que descomponerlo en una suma de potencias de 2.
Afortunadamente, 2² nos da 4, y 2¹ nos da 2. Ahora que ya no tenemos más números que descomponer, podemos convertirlos en binario. Como empezamos con 26 tenemos que preguntarnos si hemos usado esa potencia, y todas las anteriores, hasta llegar a 20.
¿Cuántas veces hemos usado 26? 1
¿Cuántas veces hemos usado 25? 0
¿Cuántas veces hemos usado 24? 0
¿Cuántas veces hemos usado 2³? 1
¿Cuántas veces hemos usado 2²? 1
¿Cuántas veces hemos usado 2¹? 1
¿Cuántas veces hemos usado 20? 0
Por tanto, 78 en binario es 1001110

No era tan difícil como pensabas, ¿verdad? El mismo algoritmo funciona para decimales de tres o más dígitos. La única diferencia es que puede que necesites una tabla de potencias de 2 más exhaustiva (o una calculadora) para trabajar con el algoritmo. O puedes usar un conversor de decimal a binario para números grandes, como el que está al principio de esta página. En resumen, convertir de decimal a binario es tan fácil como contar 1, 2, 3; o, mejor dicho, ¡1, 10, 11!
Tabla de los cien primeros Números Decimales en Binario
La siguiente tabla muestra los números decimales del 0 al 100 junto con su representación binaria.
| Número Decimal | Binario |
| 0 | 0 |
| 1 | 1 |
| 2 | 10 |
| 3 | 11 |
| 4 | 100 |
| 5 | 101 |
| 6 | 110 |
| 7 | 111 |
| 8 | 1000 |
| 9 | 1001 |
| 10 | 1010 |
| 11 | 1011 |
| 12 | 1100 |
| 13 | 1101 |
| 14 | 1110 |
| 15 | 1111 |
| 16 | 10000 |
| 17 | 10001 |
| 18 | 10010 |
| 19 | 10011 |
| 20 | 10100 |
| 21 | 10101 |
| 22 | 10110 |
| 23 | 10111 |
| 24 | 11000 |
| 25 | 11001 |
| 26 | 11010 |
| 27 | 11011 |
| 28 | 11100 |
| 29 | 11101 |
| 30 | 11110 |
| 31 | 11111 |
| 32 | 100000 |
| 33 | 100001 |
| 34 | 100010 |
| 35 | 100011 |
| 36 | 100100 |
| 37 | 100101 |
| 38 | 100110 |
| 39 | 100111 |
| 40 | 101000 |
| 41 | 101001 |
| 42 | 101010 |
| 43 | 101011 |
| 44 | 101100 |
| 45 | 101101 |
| 46 | 101110 |
| 47 | 101111 |
| 48 | 110000 |
| 49 | 110001 |
| 50 | 110010 |
| 51 | 110011 |
| 52 | 110100 |
| 53 | 110101 |
| 54 | 110110 |
| 55 | 110111 |
| 56 | 111000 |
| 57 | 111001 |
| 58 | 111010 |
| 59 | 111011 |
| 60 | 111100 |
| 61 | 111101 |
| 62 | 111110 |
| 63 | 111111 |
| 64 | 1000000 |
| 65 | 1000001 |
| 66 | 1000010 |
| 67 | 1000011 |
| 68 | 1000100 |
| 69 | 1000101 |
| 70 | 1000110 |
| 71 | 1000111 |
| 72 | 1001000 |
| 73 | 1001001 |
| 74 | 1001010 |
| 75 | 1001011 |
| 76 | 1001100 |
| 77 | 1001101 |
| 78 | 1001110 |
| 79 | 1001111 |
| 80 | 1010000 |
| 81 | 1010001 |
| 82 | 1010010 |
| 83 | 1010011 |
| 84 | 1010100 |
| 85 | 1010101 |
| 86 | 1010110 |
| 87 | 1010111 |
| 88 | 1011000 |
| 89 | 1011001 |
| 90 | 1011010 |
| 91 | 1011011 |
| 92 | 1011100 |
| 93 | 1011101 |
| 94 | 1011110 |
| 95 | 1011111 |
| 96 | 1100000 |
| 97 | 1100001 |
| 98 | 1100010 |
| 99 | 1100011 |
| 100 | 1100100 |
Preguntas y respuestas sobre convertir números decimales a binario.
El conversor de decimal a binario de ConvertBinary.com es muy fácil de usar.
Sólo tienes que seguir estos pasos: introduce tu número decimal en el primer campo, y pulsa el botón «Convertir».
La representación binaria de tu número decimal aparecerá inmediatamente en el campo de abajo.
Para convertir números decimales a su equivalente binario, tienes dos opciones: puedes usar un conversor online (como el que ofrecemos de forma gratuita en ConvertBinary.com), o puedes hacerlo manualmente.
Si quieres aprender cómo convertir de decimal a binario manualmente, puedes leer esta guía, o ver el tutorial asociado.
Primero toma el número decimal y comprueba las potencias de 2. Luego encuentra las potencias de 2 más cercanas al decimal, iguales o menores que el decimal.
Y después repite el proceso hasta que no haya resto.
El proceso es automático y tan rápido que parece instantáneo, incluso para números grandes.
¡Por supuesto! Si quieres convertir cualquier número representado en binario a decimal, puedes usar el conversor de binario a decimal de ConvertBinary.com.
El número 10 (diez) es 1010 (uno-cero-uno-cero) en binario.
Puedes encontrar una tabla de la representación en binario de los números decimales del 0 al 100 en ConvertBinary.com.
